Some weeks ago, to end an evening of board gaming, I was introduced to the Knizia roll and write called Criss Cross (or Détrak here in France). A fascinating two dimensional dice placement game with very simple rules. As we left my friends place we discussed that it should be feasible to implement a simple AI for the game. So, when I got home, I started the process…
Basic overview
The game is played on a grid of 5 by 5 squares, each round two dice are rolled and all players copies them onto their own grid according to some placement rules (that I will get back to). At the end of the game, after 12 rolls, each line scores points according to equal dice next to each other along the vertical and horizontal lines. (12 times 2 is, of course, 24, not 25, but each player start with a random die face inscribed in the upper left corner of their grid.) One of the most interesting design decisions here is the points table. For a sequence of 2 equal dice, you score 2, for 3 you score 3, for 4 it’s 8 and for 5 it’s 10. We played with the “advanced” rules that say that one of the diagonals (the one without the pre-inscribed dice) also counts (twice!) and if you have no scoring combos on any line you lose -5 points.
Scoring
First out was just the scoring functions.
To find series of numbers in a each line I used the takewhile from itertools, like so:
def find_series(l):
series = []
while len(l)>0:
if l[0]==0: # 0 is not-filled and can not form a chain
c = 1
else:
c = len(list(takewhile(lambda x: x==l[0],l)))
series.append(c)
l = l[c:]
return series
Then the scoring of lines and grids follow like this:
def score_line(line, table = {1: 0, 2: 2, 3: 3, 4: 8, 5: 10}, penalty = -5):
series = find_series(line)
if max(series) == 1:
score = penalty
else:
score = sum([table[x] for x in series])
return score
def score_grid(grid, diagonal = True, table = {1: 0, 2: 2, 3: 3, 4: 8, 5: 10}, penalty = -5):
score = 0
for axis in [0,1]:
score += sum(np.apply_along_axis(lambda l: score_line(l,table = table, penalty = penalty), axis=axis, arr=grid))
if diagonal:
score += 2*score_line(np.diag(np.fliplr(grid)),table = table, penalty = penalty)
return score
Where the ‘grid’ is simply an array of arrays.
All is randomness…
With this framework in place I wanted to see what scores would occur by pure chance…
scores = []
for _ in range(0,10000):
g = np.random.randint(low = 1, high = 6, size = (5,5))
scores.append(score_grid(g))
A quick df.describe we get this:
| stat | |
|---|---|
| count | 10000.000000 |
| mean | -6.262300 |
| std | 14.376354 |
| min | -53.000000 |
| 25% | -16.000000 |
| 50% | -7.000000 |
| 75% | 4.000000 |
| max | 54.000000 |
And, we can (mat)plot(lib) it like so:
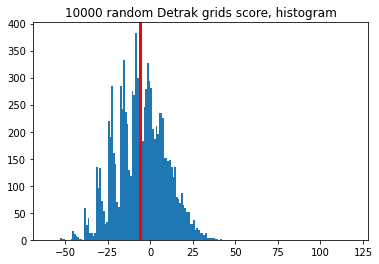
Anecdote
The night I implemented this I added a bug to my code that did the scoring… completely wrong… I ended up with a mean score of about 27(!) for these random grids – instead of negative 6.3. I was too tired to realise that that was way too high, but not too tired to fire off an email to the player that scored 20 – twice! Monkeys and Shakespear and everything! The scores were even a nice Gaussian – with hardly any noise at all… When revisiting it another day I realised that I had forgotten the score_line() part of my scoring function for the diagonal… That meant that, basically the whole score was driven by the sum of the dice on the diagonal. D’Oh!
And it checks out:
\[2 * 5 * \frac{\sum_{k=1}^6 k}{6} + \frac{12}{10} * (-6.3) \approx 27\]Other experiments
Inspired by the high scores of my (faulty) implementation, I wanted to see how tweaking the playing field would change the outcome. Here are some results – after fixing the scoring bug, though.
4x4 Grid
As expected mean of the scores was even lower on a 4 by 4 grid: -14.2.
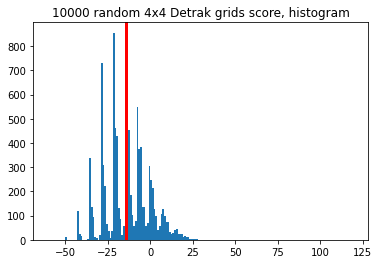
6x6 Grid
And again, as expected, higher on a 6 by 6 grid: 4.2.
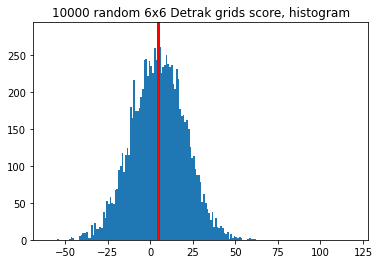
Other platonic solids
What if we use 2d4, instead of 2d6? As expected we get a higher mean: 19.5.
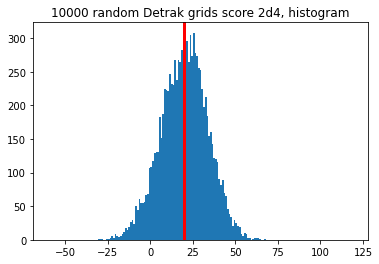
Other scoring tables
The default table lends itself to very interesting decisions during game play, but what if it was like this instead:
score_table = {
1:0,
2:2,
3:4,
4:8,
5:16
}
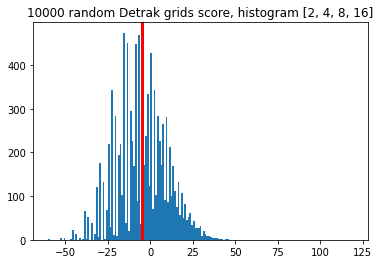
The mean ends up at about -5.0. (Not so much higher, and likely mainly driven by the increase points for 3-in-a-row.)
Summary
We’ve started our random walk towards singularity… Or, at least potential human-level AI for Criss Cross… Next up: the game state and first approaches.