Now that the scoring function was in place (see part 1) I could start working on a good old AI, but first some helper functions.
Helper functions
Some more functions are needed… One to update the grid – or a copy of it:
def place(grid, x, y, symbol, copy = True):
if copy:
grid = grid.copy()
grid[x,y]=symbol
return grid
And another one to find neighbours:
def neighbours(grid, i , j):
n = []
if i > 0:
n.append((i-1, j))
if i+1 < grid.shape[0]:
n.append((i+1, j))
if j > 0:
n.append((i, j-1))
if j+1 < grid.shape[1]:
n.append((i, j+1))
return n
And one to find valid positions for the two dice.
def valid_positions_orig(grid):
valid = []
for i in range(grid.shape[0]):
for j in range(grid.shape[1]):
if grid[i,j]==0:
for x,y in neighbours(grid, i,j):
if grid[x,y]==0:
valid.append(((i,j),(x,y)))
return set(valid)
I’ve also implemented this valid moves function:
def valid_moves_orig(grid, dice):
vp = valid_positions_orig(grid)
vm_f = {}
for pos1, pos2 in vp:
moves = {'p1': pos1, 'd1': dice[0],'p2': pos2, 'd2': dice[1]}
temp_grid = grid.copy()
temp_grid = place(temp_grid, pos1[0], pos1[1], dice[0])
temp_grid = place(temp_grid, pos2[0], pos2[1], dice[1])
# Check for symmetry...
if str(temp_grid.T) not in vm_f.keys():
vm_f[str(temp_grid)] = moves
return vm_f
And to be able to both generate random dice sequences and replay games, I wrote this generator:
def dice_pair_generator(d=6, arr=[]):
while True:
if len(arr)==0:
yield [random.randint(1,d), random.randint(1,d)]
else:
yield arr.pop(0)
Anecdote
“And so, to celebrate the beginning of holidays, I have an offer for you. Take the rules of your favourite game and read it very, very carefully, one paragraph a time. There’s a chance that you find a detail or a few proving irrefutably, that you’ve been playing it the wrong way.”
The reason for the “_orig” part of the function names above, is because, when my friend had thought us the rules to the game he had, well, interpreted them wrongly. His interpretation was that we could only place the new dice next to already existing dice in our grid, but they didn’t have to be next to each other. Whereas it is the complete opposite – one can place the dice anywhere in the grid, but they have to be orthogonally next to each other. The game actually works both ways, but I think Knizia made the correct choice in the official rules…
“Do play it according to the genuine rules. Experience the taste of freshness, discover new possibilities in your beloved board game, and name the new rules “Trzewiczek’s expansion”. It applies to any game. And you get it from me for free.”
So, “Florent’s variant”, then.
Monte Carlo
The first thing I wanted to try, encouraged by my bug in the scoring function, was just to score each move based on randomly filling the rest of the grid n times and keeping the best move, so I implemented this random fill function. (There is probably a way to matrixify this, but this works for now.)
def random_fill(grid, values):
for i in range(grid.shape[0]):
for j in range(grid.shape[1]):
if grid[i,j]==0:
grid[i,j]=random.choice(values)
return grid
Then the heart of the simulation is this piece:
for move in valid_moves:
grid_mark = place(grid, move['p1'][0], move['p1'][1], move['d1'])
grid_mark = place(grid_mark, move['p2'][0], move['p2'][1], move['d2'], False)
scores = []
for _ in range(iters):
grid_temp = random_fill(grid_mark, list(range(1,7)))
temp_score = score_grid(grid_temp, penalty = penalty, diagonal = diagonal)
scores.append(temp_score)
score = pd.DataFrame(scores).describe().loc[ strategy , : ][0]
if score>best_score:
best_move = move
best_score = score
Basically we complete the grid n times per valid move and keep the one that scores the best. The strategy variable here can be any variable in the describe function of pandas. ([‘count’, ‘mean’, ‘std’, ‘min’, ‘25%’, ‘50%’, ‘75%’, ‘max’]) I wanted to see if this could serve as a proxy for the AI’s approach to risk taking. (‘max’ and ‘min’ are quite chaotic, but ‘75%’ turned out to be a nice compromise…)
Super basic, but, given the wrong rules outlined above I got the mean from -6 to about 17.
Simulation
Next up was to simulate the valid moves, score them ‘locally’, and keep the best move.
for move in vm:
grid_mark = place(grid, move['p1'][0], move['p1'][1], move['d1'])
grid_mark = place(grid_mark, move['p2'][0], move['p2'][1], move['d2'], False)
score= score_grid(grid_temp, penalty = penalty, diagonal = diagonal)
if score > best_score:
best_move = move
best_score = score
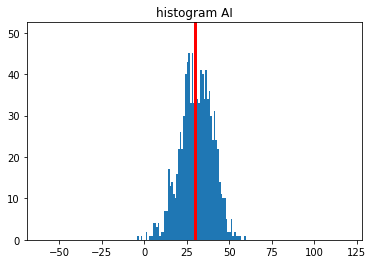
And lo and behold, the mean went up from 17 to 30.5!
| stat | |
|---|---|
| count | 10000.000000 |
| mean | 30.491000 |
| std | 9.092777 |
| min | -8.000000 |
| 25% | 25.000000 |
| 50% | 31.000000 |
| 75% | 37.000000 |
| max | 60.000000 |
“Hybdrid” approach
OK. Promising. I then moved on to a kind of hybrid approach, where, for each valid move I score the resulting grid, before keeping the n best ones and random fill them to calculate a hybrid score.
Like so:
scores_arr = []
for move in vm:
grid_mark = place(grid, move['p1'][0], move['p1'][1], move['d1'])
grid_mark = place(grid_mark, move['p2'][0], move['p2'][1], move['d2'], False)
scores_arr.append({ 'move': move, 'score': score_grid(grid_mark, penalty = penalty, diagonal = diagonal), 'grid': grid_mark })
scores_arr = sorted(scores_arr, key=lambda x: -x['score'])[:max_width]
for temp_score in scores_arr:
move = temp_score['move']
_, _, grid_temp = get_best_move(grid = temp_score['grid'].copy(), vm = None, strategy = '75%', iters = iters, recursive = recursive, depth = depth+1, max_rec_depth = 1)
score_mark = score_grid(grid_temp, penalty = penalty, diagonal = diagonal)
score = (temp_score['score']*2 + score_mark*1)/3
if score > best_score:
best_move = move
best_score = score
As you might see, I decided to weigh the ‘local’ score a bit higher (2/3) than the simulated score (1/3) – one bird in the hand is better than ten on the roof, as we say…
And lo and behold, the mean went up from 30.5 to 31.5!
| stat | |
|---|---|
| count | 100.00000 |
| mean | 31.53000 |
| std | 7.97275 |
| min | 10.00000 |
| 25% | 27.75000 |
| 50% | 32.00000 |
| 75% | 37.00000 |
| max | 50.00000 |
Summary
Not too bad, but still, not human level, as our analogue winning scores were hovering around 40… (Again, this is using ‘Florent’s variant’ rules as outlined above, and is not comparable to scores in the real game.) Next up: recursion!